Um problema aparentemente simples, mas que permanecia sem solução por quase 50 anos, foi solucionado pelo matemático Richard Schuwartz, da Universidade Brown, na cidade de Providence nos EUA. A questão respondida foi: qual é o menor tamanho possível para se fazer uma fita de Möbius de papel?
Para quem não está ligando o nome ao objeto, vale a pena citar alguns exemplos famosos de fitas de Möbius, como o símbolo internacional de reciclagem e o logotipo do Google Drive. A principal característica desse curioso objeto matemático é que ele só tem uma superfície e uma borda. Ou seja, é uma fita de papel comum que você torce uma vez e cola as pontas.
Mas, apesar dessa provável simplicidade, o conceito dessas fitas envolve propriedades complexas e, desde que foram descritas em 1858 pelos matemáticos alemães August Möbius e Johann Listing, são objetos de fascínio de matemáticos, físicos e artistas. No campo prático, as faixas de Möbius são usadas em gravadores, máquinas de escrever, correias transportadoras, cartuchos de impressão e montanhas-russas.
A proporção ideal para se fazer uma fita de Möbius
Na verdade, uma solução para o problema das tiras de Möbius já havia sido proposta em 1977, pelos matemáticos Charles Sidney Weaver e Benjamin Rigler Halpern. Eles afirmaram que a relação entre o comprimento e a largura do papel deve ser superior a √3, ou cerca de 1,73. No entanto, a dupla não conseguiu provar sua hipótese, que ficou conhecida até agora como "conjectura de Halpern-Weaver".
Quando Richard Schwartz, o autor da suposta solução atual (o artigo ainda não foi revisto por pares), leu que uma tira de Möbius com um centímetro de comprimento precisaria ser mais larga que √3 ou 1,73 cm, ficou imediatamente “viciado” no problema. Ele fez várias tentativas de resolvê-lo, até mesmo em um artigo de 2021, cuja abordagem acabou falhando.
Resolvendo a conjetura ótima da fita de Möbius
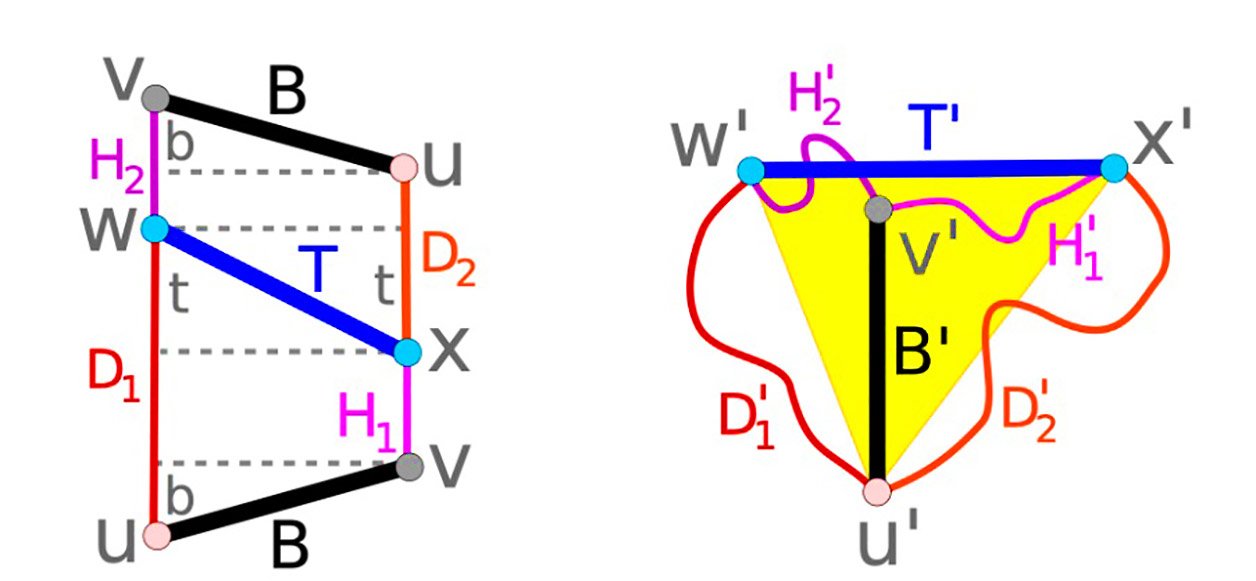Cortar uma tira resultou em um trapézio.Fonte: Richard Evan Schwartz
Passando noites sem dormir por não ter resolvido o problema, Schwarts o retomou recentemente e começou a amassar fita de Möbius de papel, na expectativa de que uma forma em 2D lhe desse algum insight. E foi o que aconteceu: cortando um desses loops para formar um ângulo, ele percebeu que o papel não parecia um paralelogramo (como ele havia relatado em seu artigo anterior), mas sim um trapézio.
“Embaraçosamente, descobri recentemente que cometi um erro ao configurar o problema de otimização”, escreve Schwartz em seu artigo. Aí, com ajuda de alguns colegas, ele corrigiu sua falha e encontrou o que chamou de “uma prova realmente excelente” para a etapa intermediária, que resultou em uma simplificação do artigo.
Em um misto e surpresa, Schwarts refez suas contas, mas desta vez resolvendo corretamente o problema da otimização. E, desta vez, "acertei... √3 na mosca!", ele conclui.
Ficou com alguma dúvida? Conte para gente em nossas redes sociais e aproveite para compartilhar o matéria com os seus amigos.
Fontes
Categorias
